はじめに
DJが、ハーモニーミキシングをするために理解しておいた方が良い、サークル・オブ・フィフス(五度圏)までの道のりもいよいよ今回でラストです。
あなたはきっと前回までの内容で、長調、短調、そして音階について理解できたと思います。
もしまだ理解しきれていない方や、初めてこの記事にたどり着いた方は以下の記事からご覧下さい。
 【音楽基礎知識】DJも知っておいて損なし!! 音階と調について<長音階編>
【音楽基礎知識】DJも知っておいて損なし!! 音階と調について<長音階編>  【音楽基礎知識】DJも知っておこう!音階と調について<短音階編>
【音楽基礎知識】DJも知っておこう!音階と調について<短音階編> では、おさらいとして、長音階は『全音、全音、半音、全音、全音、全音、半音』で、短音階は『全音、半音、全音、全音、半音、全音、全音』という音階でしたね。

そして、これらで各音階を作ることで、全てを合わせると24の音階ができることが分かりました。
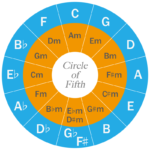
しかし、長音階と短音階が分かっただけでは、まだハーモニーミキシングはできず、サークル・オブ・フィフスを完全に理解できるまでには至っていません。
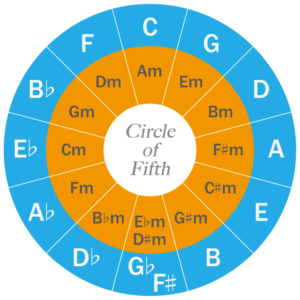
調号が無造作に並んでいるように見えるこの円には、ある法則性があるのです。
それを今回は紐解いていきましょう。
まだまだ学ぶべきことがいくつかありますが、一つ一つゆっくりと覚えていってもらえたらと思います。
音と音の距離を測るには?

当然の事ながら、鍵盤の一つの音から離れた音との間には距離が作られます。
それはごく近い隣の場合もあれば、遠く離れている場合もあります。
そのため、これらの音と音の距離を測るには、分かりやすい指標が必要です。
その指標を音楽では『度数』という言葉で表します。
度数は、音と音のお互いの距離を測るためには欠かせず、次にどの音を鳴らすかという重要な単位となってくれるものです。
例えば、今まで数えてきた『全音』や『半音』だけでは、元になる音からどれだけ距離が離れているかは、いくつあるかその数を数えなければ分かりません。
ただ、そんなことをいちいち行うのは不便でしかなく、それに代わって数えられる『何か』があったほうが便利なことは、誰にとっても明らかです。
そういった意味で、度数は非常に有効な数え方になっています。
では、その度数について早速説明していきましょう。
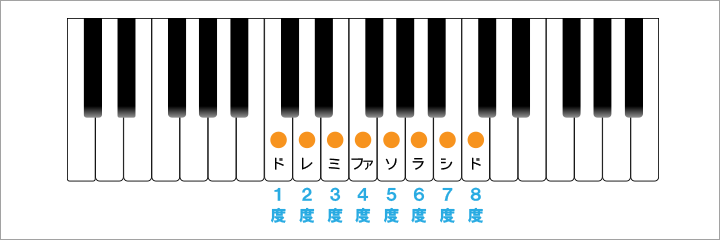
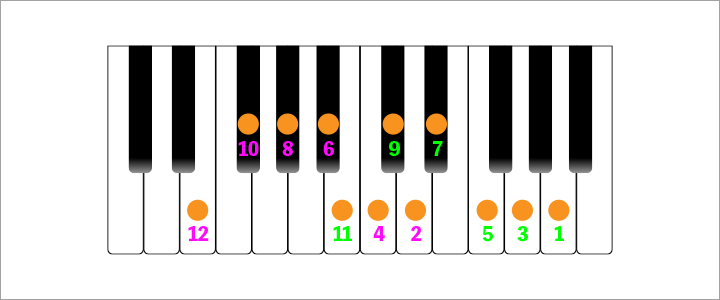
度数は、『1度、2度、3度、4度、5度、6度、7度、8度』という数を基本にしています。(他にも、9度から上の度数もありますが、この記事では重要ではないので割愛しておきます)
最初の1度は、その音階上の最初の音であり、例えば、ハ長調なら『ド』、ニ長調なら『レ』が1度となります。
次に大きく飛ばして、最後の8度を見てみます。
この8度という度数は、1度の1オクターブ高い音になるので、ドならドということになります。
1度と8度については、特に難しくはないですね。
一方、2度から7度までの度数は、1度から8度までの間の距離を表しているので、音を測る上では重要な度数たちです。
そして、これらの度数には一つ一つ言葉を付けることで、より正確な音の距離を測れるようにされており、『減』、『短』、『長』、『増』、『完全』という5つの言葉が用いられています。
これらの言葉は、各度数の頭に付けられるものですが、その度数によって使われる言葉は変わってきます。
以下のような具合です。
- 完全=1度、8度
- 完全、減、増=4度、5度
- 減、短、長、増=2度、3度、6度、7度
音の距離を測る度数の意味

さて、これらの度数と付けられる言葉の説明ですが、分かりやすい『ドレミファソラシド』のハ長調で考えていくことにします。
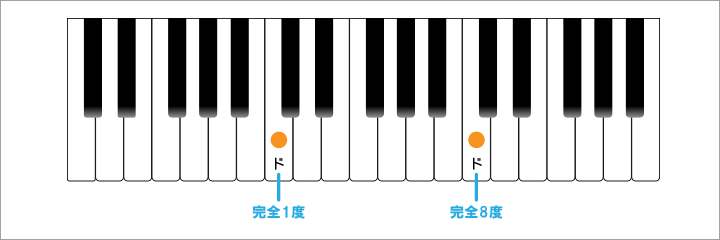
ハ長調の1度と8度は低い『ド』と高い『ド』であり、『完全1度』、『完全8度』という言葉となり、単純です。
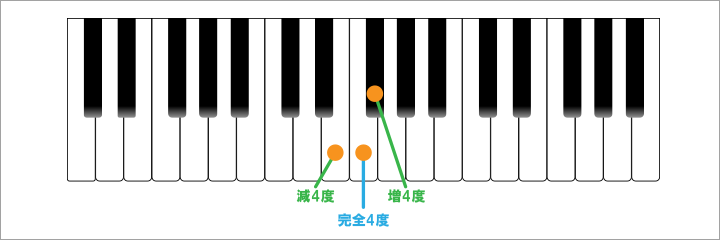
次にハ長調の4度と5度は、それぞれ『ファ』と『ソ』に該当しますが、これらも1度と8度と同様に基本的には『完全』という言葉が付けられます。
ただ、そこからさらに一つ高い音を表す場合は『増』という言葉が付き、一つ低い音を表す場合には『減』という言葉が付けられるようになります。
例えば、完全4度がファであれば、減4度はミであり、増4度はファ♯となります。
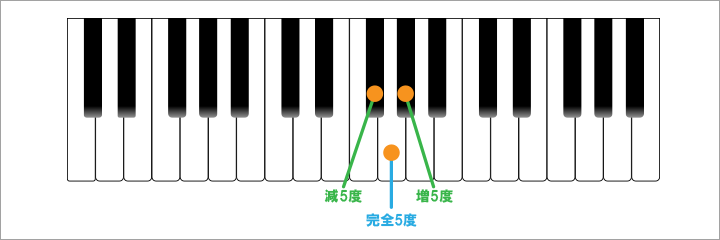
また、完全5度がソであれば、減5度はファ♯であり、増5度はソ♯となります。
次は、2度、3度、6度、7度という度数になりますが、これらは『完全』という言葉のように一つの言葉だけで音を明確に表すことはなく、基本的に『長』と『短』という2つの言葉を用います。
そして、そこからの音の高低を表す場合に『増』と『減』が追加で使われるようになってきます。
例として…
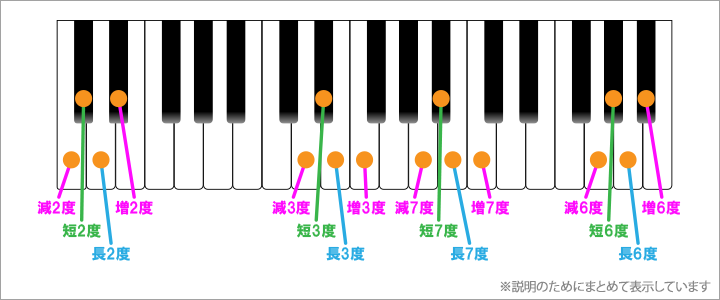
- ハ長調の2度の場合は、長2度がレとなり、短2度がレ♭、減2度はドで完全1度と同じ音になり、増2度はレ♯になる
- ハ長調の3度の場合は、長3度がミとなり、短3度がミ♭、減3度はレで長2度と同じ音になり、増3度はファになる
- ハ長調の6度の場合は、長6度がラとなり、短6度がラ♭、減6度はソで完全5度と同じ音になり、増6度はラ♯になる
- ハ長調の7度の場合は、長7度がシとなり、短7度がシ♭、減7度はラで長6度と同じ音になり、増7度はドになる
このように、2度から7度は、1度、4度、5度、8度とは違い、少々複雑になってくるので注意が必要です。
また、上記のように度数によっては同じ音がかぶる場合がありますが、そのことを『異名同音』と呼ぶのでこれもついでに覚えてしまうと良いでしょう。
ここで1つ注意点として、どの度数に関しても、鍵盤の数を表すわけではないことに気をつけなければいけません。
例えばミの長3度上の音は?と問われた際にミからの白鍵を3つ数えて、ソと答えると間違いになってしまいます。
この場合、正しくはソ♯であり、きちんと全音2つ分数える必要があるということを覚えておきましょう。
音階上の音を表す言葉

度数が分かった上で、次は音階を表している言葉があることを知っておきましょう。
どの音階でも構わないのですが、一つの音階の中には4つの重要な音があり、それを表すための言葉が付けられています。
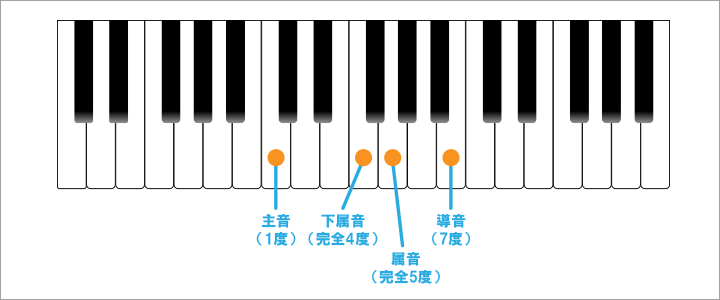
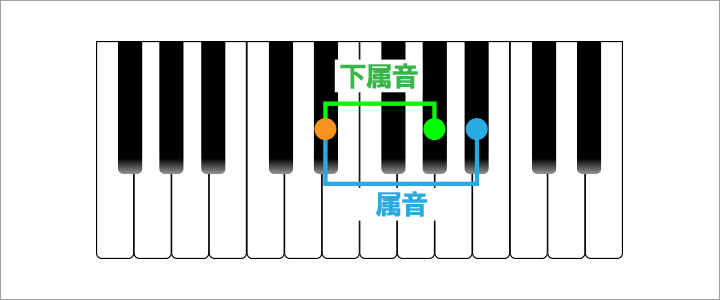
それらを『主音(しゅおん)』、『属音(ぞくおん)』、『下属音(かぞくおん)』、『導音(どうおん)』と呼びます。
『主音』は音階の第1音を指し、その響きから、いつでも帰れる家のような存在の音とされています。
『属音』は第5音(完全5度)を指し、その音階の中で支配的な音の響きをしていることを表しています
『下属音』は第4音(完全4度)を指し、その音階の中で属音に次いで支配的な音の響きをしていることを表します。
『導音』は第7音を指し、この音は不安的な音とされ、主音に引っ張られるような響きを持っているため、このような名前が付けられています。
これら4つの音は音階の中では必要不可欠であり、それぞれが役割を担っている音になっています。
ただ、その効果は単音の響きだけでは分かりづらく、実際にはコードを作る際に顕著に現れるものになってきます。
調には近い調と遠い調がある

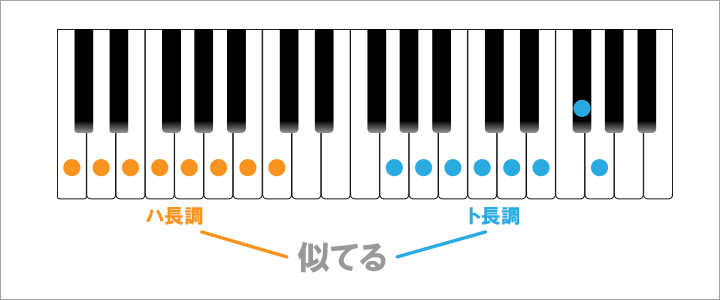
ある調とある調を比べた際に、その関係性が近いか遠いかを判断することができます。
例えば、ハ長調とト長調は構成している音が1音(ファ)以外同じなので、関係性が極めて近いと言えます。
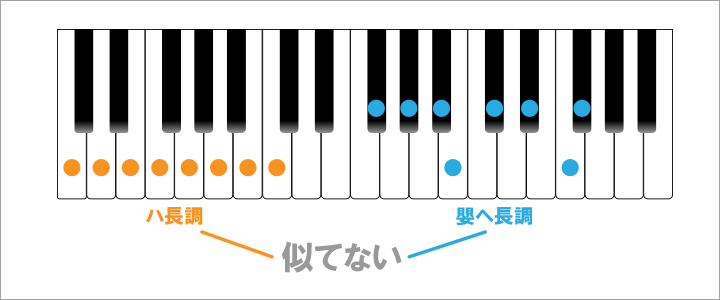
反対に、ハ長調と嬰へ長調などは、1音(シ)しか同じものがなく、関係性が極めて遠いと言えます。(嬰へ長調のファはミに♯が付いた異名同音)
このように、元になる調と比べて共通する音が多い調のことを『近親調』と呼び、共通する音が遠い(少ない)調のことを『遠隔調』と呼びます。
そして、近い調である近親調については、どのように近いかを表すためにさらに種類が分けられています。
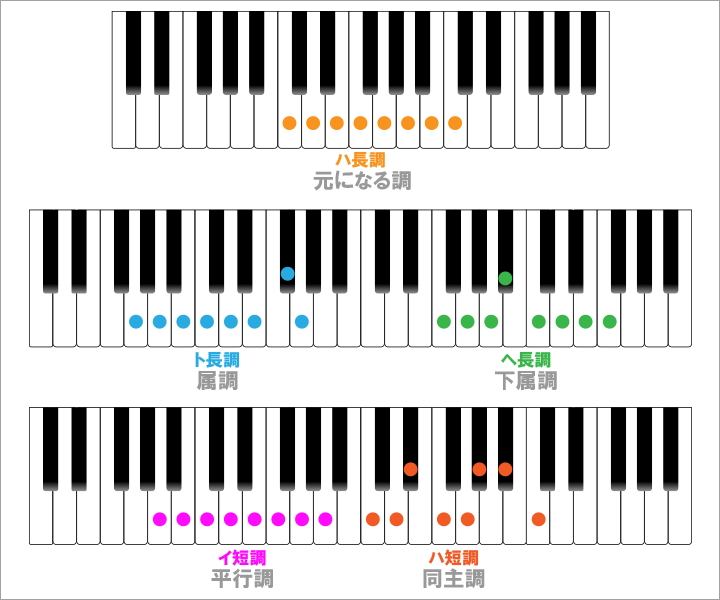
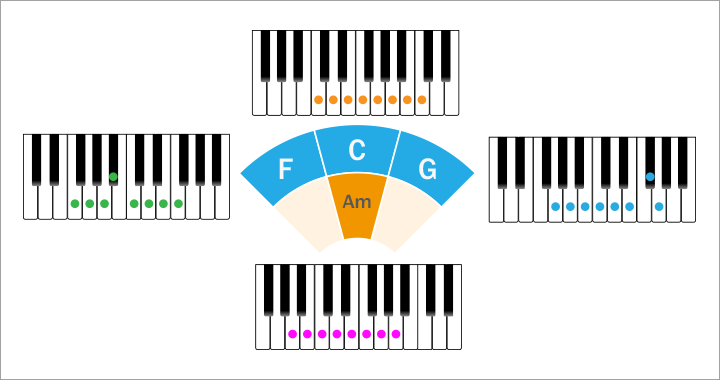
それは『属調』、『下属調』、『平行調』、『同主調』という4つのものです。
また、属、下属という言葉がでてきましたね。
- 属調とは、元になる調の完全5度上の音から始まる調(ハ長調だったらト長調)のことを指します。
- 下属調とは、元になる調の完全4度上の音から始まる調(ハ長調だったらヘ長調)
- 平行調とは、元になる調と同じ構成音で表す異なる調(ハ長調だったらイ短調:逆もしかり)
- 同主調とは、元になる調の主音から始まる異なる調(ハ長調だったらハ短調)
長音階の属調を求める方法

さて、度数やその音の種類や名前が出揃ってきましたね。
サークル・オブ・フィフス(五度圏)を理解するという目的に段々と近づいて来ていますよ。
とはいえ、まだ確信まで迫りきれてはいないので、このまま続けていきましょう。
次に必要なのは、長音階と短音階を合わせた24の調を求める方法です。
分かりやすいようにハ長調(C)から進めていきます。
C(ド)は元になる調なので、Cの属調(完全5度)から求めていきますが、それがG(ソ)だということはすぐに分かりますよね?
主音(ここではド)から完全5度を、『全全半全』と長音階で数えるだけですよ。
次に、同じようにGの属調を考えてみましょう。
G(ソ)を主音にした場合の属音はD(レ)になりますね。
難しくはないと思います。
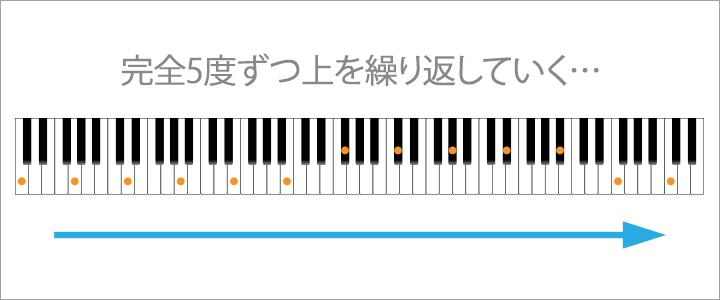
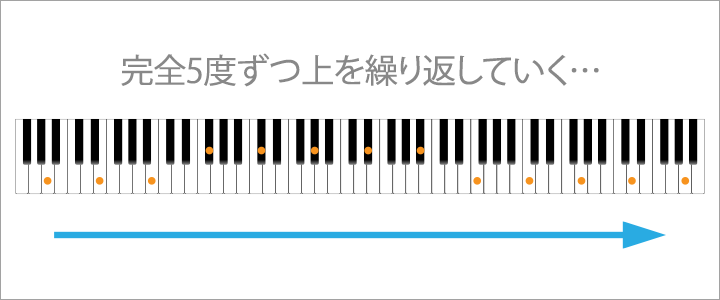
そして、この方法で完全5度ずつ上をさらに繰り返していくと…
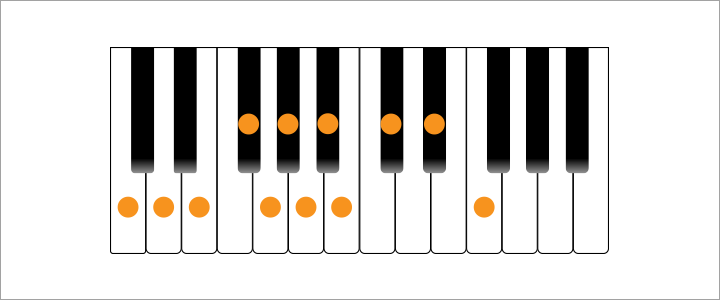
C → G → D → A → E → B → F♯(G♭) → D♭ → A♭ → E♭ → B♭→ F → C
という順番になることが分かります。
鍵盤で表すとこのようになります。
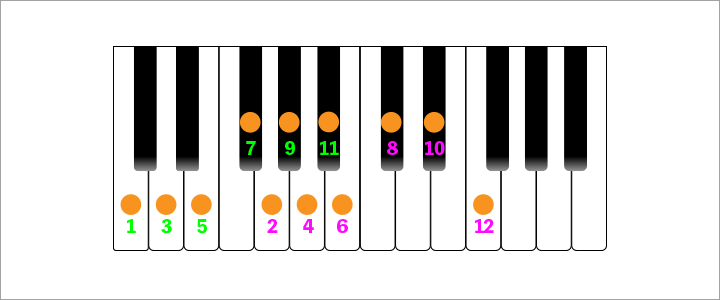
ちょっとあまりに横長なのでコンパクトにまとめてみますか。
するとこのようになります。
さぁこの図を目を凝らしてじっくり見てみましょう。
何となく法則性らしきものが見えてきませんか?
それは、属音に登ったあとに次に求めたい属音は、5度前の音から全音高い音がその順番になってくるというものです。
言葉じゃ全くもって分かりづらいですねw
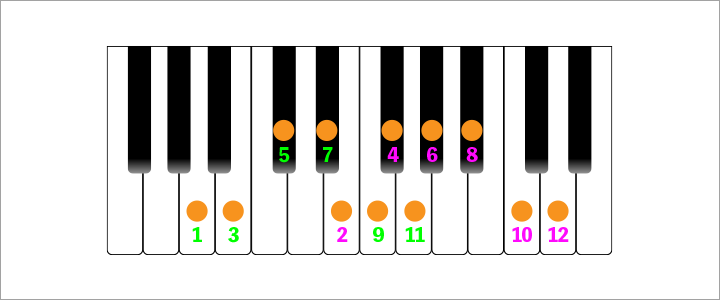
なので、以下を見てください。
何だかこの図を見ると目から鱗な感じがしてきませんか?
そう、属調を求めてようとしていくと、自ずと音階を行ったり来たりを繰り返すことになるのです。
この完全5度ずつ移動するイメージを視覚的に覚えてしまうと、何かと捗ることになります。
覚え方のコツは、基本的に白鍵の属音(完全5度)は白鍵になるし、黒鍵の属音は黒鍵になることを知ることです。
ただ例外として、白鍵シの属音は黒鍵のファ♯、黒鍵ラ♯の属音は白鍵ファになることだけは頭に入れておきましょう。
あと注意点もあり、Fの次はCに戻ることは忘れないことです。
まぁもし不安になったら、自分で5度分ずつ数えてもらえれば分かるはずです。
そう、心配になったらいつでも全全半全と数えればいいのです。
長音階の下属調を求める方法

上記では完全5度上の音の求め方が分かりました。
次は、反対の下属調である完全5度下の下属音を考えていきましょう。
ここで注意すべきことは、先ほどの5度上の音とは同じにはならないことです。
1オクターブ内の音階は偶数ではなく、7音という奇数であることを忘れてはいけません。
では、Cから逆に全全半全と低い音に向かって数えてみてください。
Cの完全5度下はG(ソ)ではなく、F(ファ)になりますよね?
ちょっと混乱しがちですが、仕方がありません。
ただ、そんなに頭を悩ますことも実はありません。
基本的には、ある音から5度上という音は、高い音でも低い音から見ても変わらないからです。
これも言葉では分かりづらいですが、つまり、Cの完全5度下はFではあるものの、裏を返せばFの完全5度上はCであるというものです。
これもすんなりイメージできてしまえば、非常に早く考えられると思います。
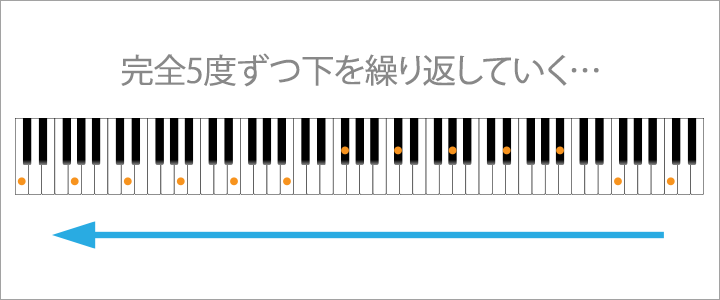
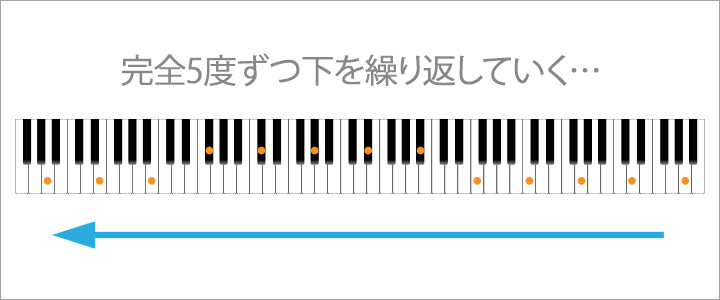
ではこの完全5度下を繰り返しながら順番に並べていきましょう。
すると…
C → F → B♭ → E♭ → A♭ → D♭ → F♯(G♭) → B → E → A → D → G
鍵盤で表すとこのようになりますね。
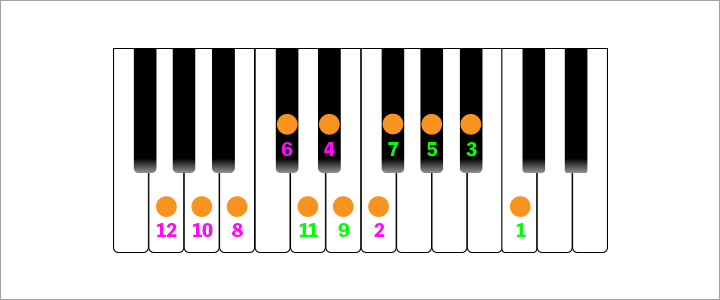
こちらも横長なのでコンパクトにまとめてみましょう。
こちらも、5度上と同じような行ったり来たりの移動に見えますね。
そして、ここまでの5度上の順番と5度下の順番には法則があることも分かったはずです。
5度上に進む音階は以下です。
C → G → D → A → E → B → F♯(G♭) → D♭ → A♭ → E♭ → B♭→ F → C
(分かりやすくするために最後に元に戻るCを付け加えています)
これを逆から読むと
C → F → B♭ → E♭ → A♭ → D♭ → F♯(G♭) → B → E → A → D → G → C
と、このようになり、5度上と5度下の順番はただ正反対になっているだけなのです。(上記の横長の画像2つが全く一緒ですからね)
それで、これが何を表すかというと、サークル・オブ・フィフスの図と照らし合わせてみると分かるはずです。
外側の長調の円が、5度上なら右回り、5度下なら左回りに正にぴったりとハマり、一周しているのです。
さぁ、また面白くなってきましたね!
短音階の属調と下属調を求める方法

次に短音階も求めていきましょう。
ハ長調と平行調であるイ短調(Am)から進めます。
Am(ラ)の属音である完全5度上は何でしょう?
そう、Em(ミ)ですね。
そして、そのEmの完全5度上はBm(シ)になりますね。
同じように、またこれを完全5度上ずつ繰り返していきましょう。
すると…
Am → Em → Bm → F♯m → C♯m → G♯m → D♯m(E♭m) → B♭m → Fm → Cm → Gm → Dm
という順番になることが分かります。
こちらも鍵盤で表すとこのようになります。
それをコンパクトにするとこうなります。
次に、今度は下属調を求めるために完全5度ずつ下に向かっていきましょう。
Am(ラ)の完全5度下の下属音はもうお分かりのようにDm(レ)ですね。
そして、そのDmの完全5度下になる音はGm(ソ)になります。
さらに、こちらも完全5度下ずつを繰り返しながらまとめてみると…
Am → Dm → Gm → Cm → Fm → B♭m → D♯m(E♭m) → G♯m → C♯m → F♯m → Bm → Em → Am
となります。
またコンパクトにするとこうなります。
これが短音階上の完全5度下に向かう下属調の音階というわけです。
そして、この短音階の下属調も反対から読むと…
Am → Em → Bm → F♯m → C♯m → G♯m → D♯m(E♭m) → B♭m → Fm → Cm → Gm → Dm → Am
となり、またサークル・オブ・フィフスの図と照らし合わせてみましょう。
今度は内側の短調の5度上が右回りになり、5度下が左回りにぴったりとハマり、一周できることが分かります。
つまり、これで属調、下属調、そして平行調の関係性が網羅できたことになります。
平行調の求め方

上記までに関係性は網羅されましたが、実は長調と短調、つまり平行調についての求め方はまだできていません。
例えば、ハ長調は分かっていたとしても、そこから平行調の短調は何になるのか?という疑問です。
これを暗記する方法もあるでしょうが、実は簡単な方法もあります。
もうお分かりかもしれませんが、長調と短調の平行調になる関係性は短3度の移動で求められるのです。
つまり、元が長調なら短3度下が短調、反対に短調が元なら短3度上が長調になるわけです。
例えば、ハ長調から見て平行調を求めたいときは、Cメジャー(ド)から短3度下がその平行調になるわけで、その答えはAマイナー(ラ)になります。
反対に、Aマイナーからの平行調を求めたい場合は、短3度上を見ればそれがCメジャーだということです。
どうでしょう?特に難しくないですよね?
さぁ、これであなたは、長調からも短調からも平行調を求めることができるようになったわけです。
これで、調についてほとんどのことが理解できたはずです。
もうなんか自分のことをすごいと思いません?
属調と下属調を求めるちょっと簡単な方法

元になる調から属調を求めるには完全5度上を見れば良く、下属調を求めるには完全5度下を見れば答えがでることが分かりました。
ただ、これを少しだけ簡略化させましょう。
それは属調を求めた後、下属調もすぐに求められるようになるものです。
ハ長調であるCの属調がGであること、そして下属調はFであることは、何度も行なっているのでもう大体分かるでしょうから、例えば嬰ニ長調であるD♯の属調を求めてみましょうか?
これはA♯ですね。
では、D♯の下属調は?
この時に、もう1度D♯から完全5度下に数えるのも悪くはないのですが、ちょっと面倒ですよね?
そこで、もう少し簡単な方法があります。
それは、実は求めた属調の音から全音低い音そのものが、下属調になっているということです。
D♯の属音はA♯でしたよね。
そのA♯から全音低い音はG♯です。
つまり、D♯の下属音はG♯になるというわけです。
これは反対に下属音を求めた後に属音を求める際にも応用できます。
その場合は、下属音を求めたあとに、そこから全音高い音が属音になるということです。
繰り返しますが、半音ではなく全音であることに注意ですよ。
これを覚えておくと、属調も下属調も比較的求めやすくなると思います。
なんだかんだ言って、結局鍵盤自体を覚えておかないとね

さぁ、これで上記までの内容が全てサークル・オブ・フィフスに当てはまるようになったわけですが、最後に問題が一つ残されています。
それは、ここまできておいて何ですが、実は鍵盤の配置を記憶していないと属調も下属調も何も出てこないということです。
例えば、Gの属調となるキーは何だっけ?となった場合、鍵盤を覚えていないとその位置も何も出せないのです。
これは正直大きな問題であると言えますが、ただ、こればっかりは頭の中に鍵盤のイメージを持つしかないでしょう。
従って、可能なら鍵盤をいつでも頭の中に思い出せるようにしておくことが、やはり近道であると言えます。
また、前述したコツとして、基本的に白鍵の5度上も下も白鍵で、黒鍵の5度上も下も黒鍵になることを覚えておくと良いと思います。
その際の例外として、B(白鍵)の5度上はF♯(黒鍵)で、B♭(黒鍵)の5度上はF(白鍵)になることだけは注意してください。
あとは、鍵盤を弾けなくても構わないので、何度もその配置を見てイメージを頭に焼き付けることをおすすめします。
これで最後!サークル・オブ・フィフスの求め方!

DJとしてハーモニーミキシングをしたければ、同じ調か平行調が一番良く、元になる調に似た曲にするのであれば、属調か下属調になる曲を探せば違和感が少ないわけです。
では、まずは簡単な平行調の求め方からまとめていきましょう。
平行調は、元になる調ともう1つの調(音階)の構成音が全く同じである一方、長調(メジャー)だったら短調(マイナー)、短調だったら長調になります。
そしてその求め方は、元になる調が長調なら短3度下が短調であり、反対に元になる調が短調だったら短3度上が長調になります。
例えば、ハ長調だったらイ短調、嬰ニ短調だったら嬰へ長調が平行調になります。
次に、属調です。
属調は、元になる調の完全5度上の音から始まる調のことであり、この場合は長調なら長調のままで短調なら短調のままで変わりません。
そして下属調は、元になる調の完全5度下の音から始まる調のことであり、この場合も長調なら長調のまま、短調なら短調のままです。
属調が分かってしまえば、下属調は属調の音の全音下の音から始まり、下属調が分かれば属調はその音の全音上の音から始まります。
これらを元にしてサークル・オブ・フィフス(五度圏)の表は作られ、音楽を嗜む人にとっての一つの指標となっているわけです。
まとめ
ここまでお疲れ様でした!
色々と分かっていただけたでしょうか?
今まで長かったですが、これでサークル・オブ・フィフスという図がある理由と意味が理解できたかと思います。
そして、音楽に関する様々な知識も得られたのではないでしょうか?
もしまだ頭の中に?が並んでいるのであれば、何度も読み返して少しずつ理解していってもらえればと思います。
そして、あなたが得たここまでの知識を元に、DJプレイにハーモニーミキシングを生かしてみてください。
もちろん、これらの知識はDJだけでなく音楽の基礎としても十分活用できるはずなので、今以上に音楽を好きに、そして曲に対しての愛情を深めてもらえればと思います。
DJでハーモニーミキシングの実際のやり方についてはこちらから…
 DJでもっと綺麗に曲を繋ぐために Keyを使ったハーモニーミキシングに挑戦!
DJでもっと綺麗に曲を繋ぐために Keyを使ったハーモニーミキシングに挑戦!